Strengthen early math skills at home or school with this fun snowflake design activity. All you need is paper (such as computer, construction, or scrap paper), scissors, and something to write with. As children craft their snowflakes, explore counting, symmetry, shapes and shape composition, and space and place.
Step 1: Make a paper square.
First prepare your paper so that it’s shaped like a square. The equal sides of each square make sure each snowflake will be symmetrical after you’re done cutting. If using a standard piece of rectangular paper, take one corner and fold it diagonally to the straight edge. Then trim the strip of paper on the bottom. You could also use a ruler to measure equal lengths on all four sides of the square.
Step 2: Fold the paper into a triangle.
Once you have the paper square, fold it in half diagonally to form a triangle. Repeat this step two more times so that you end up with an even smaller folded triangle.
[Watch our video above for step-by-step instructions.]
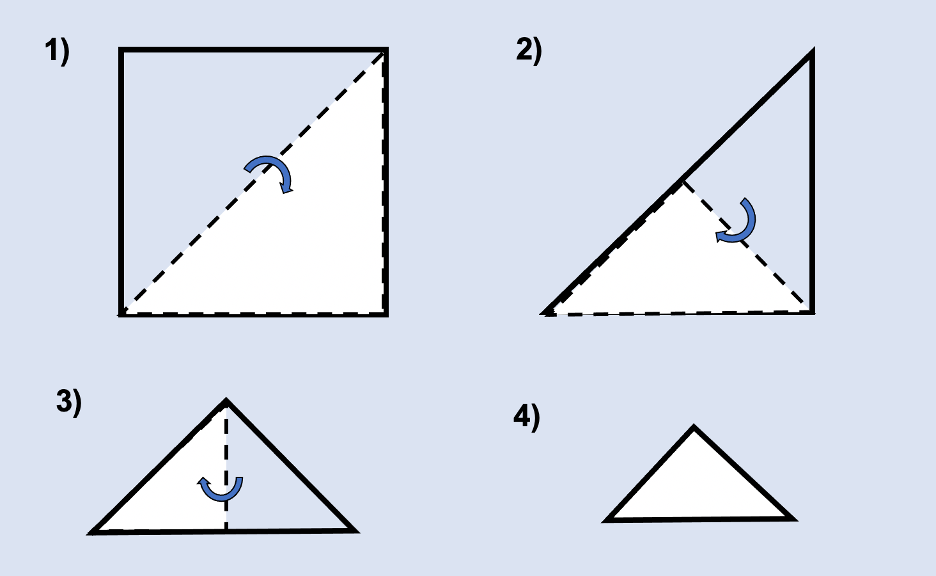
Step 3: Cut the folded triangle.
Draw lines, curves, and shapes around the edges of your folded triangle and then cut them out. As you do this, look for opportunities to notice and talk about early math concepts, including:
- Counting. Count how many individual pieces of paper are stacked in the folded triangle (e.g., two if folded once; four if folded twice).
- Shapes. Notice if the shapes you cut in the folded triangle change when you unfold the triangle.
- Shapes and spatial relations. Cut a quarter of a circle along the edge of one folded triangle. Then ask children to predict what this “pie piece” shape will look like when it’s unfolded. Practice doing this until you unfold a full circle!
- Making predictions. After cutting but before opening the folded triangle, predict how many shapes will result from cutting just one line or shape. “When I open this piece of paper, how many little triangle shapes will there be? How can we figure it out? Let’s open and see.” Then refold and continue cutting.
- Size. Use different sizes of paper to make bigger and smaller snowflakes.
- Counting and measurement. Figure out how many snowflakes you have room to hang in your windows by counting or measuring the space. What happens if you make the snowflakes bigger or smaller?
As you work, try to avoid cutting too much from the point that joins all the folded sides. If you accidentally do so, explore what happens to the design!

Ideas for Adjusting the Challenge
The amount of learning support children will need to do this activity varies.
If this activity is too challenging, we suggest you:
- Show pictures of simple paper snowflake designs as examples (you can even use the ones in this blog post!).
- Have children describe whether to add a line, curve, triangle, or other shape and how many of each to cut along each side. Then draw and complete the design together.
If this activity is not challenging enough, we suggest encouraging children to:
- Draw shapes they are less familiar with (e.g., rhombus).
- Create lines or shapes of specific lengths with a ruler.
- Figure out if cutting a triangle will make a different shape when the paper is opened.
- Answer the fun questions in this Snowflake Art Challenges PDF download.
Step 4: Unfold and enjoy your snowflake!
There are also opportunities to talk about math while admiring your snowflake creations, including ideas about:
- Symmetry. Sometimes snowflakes are symmetrical, meaning that if you fold the paper in half, the snowflake is the same on both sides. Depending on the design, there might be more than one line of symmetry on the snowflake. “Is your snowflake symmetrical?”
- Spatial relations. “What shape is right here in between these two triangles? How can we be sure it is that shape?
- Size. “Which snowflake is biggest?”
- Number. “How many triangles are on your snowflake?”
- Pattern. “I see a pattern on your snowflake. What pattern did you create? What comes next in your pattern?”
Creating paper snowflakes is one example of how math conversations with children can be integrated into many activities, routines, and play. These interactions may benefit children’s math learning and development, and their feeling that math is interesting and enjoyable!



